En matemáticas y estadística una media o promedio es una medida de tendencia central que según la Real Academia Española (2001). Resulta al efectuar una serie determinada de operaciones con un conjunto de números y que, en determinadas condiciones, puede representar por sí solo a todo el conjunto». Existen distintos tipos de medias, tales como la media geométrica, la media ponderada y la media armónica aunque en el lenguaje común, el término se refiere generalmente a la media aritmética.
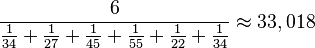
Ejemplos de medias
Media aritmética
La media aritmética es un promedio estándar que a menudo se denomina "promedio".
La media se confunde a veces con la mediana o moda.
Media aritmética ponderada
A veces puede ser útil otorgar pesos o valores a los datos dependiendo de su relevancia para determinado estudio. En esos casos se puede utilizar una media ponderada. Si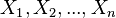 
es un conjunto de datos o media muestral y 
son números reales positivos, llamados "pesos" o factores de ponderación, se define la media ponderada relativa a esos pesos.
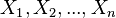es un conjunto de datos o media muestral y son números reales positivos, llamados "pesos" o factores de ponderación, se define la media ponderada relativa a esos pesos.Media geométrica
La media geométrica es un promedio muy útil en conjuntos de números que son interpretados en orden de su producto, no de su suma (tal y como ocurre con la media aritmética). Por ejemplo, las velocidades de crecimiento.
Media armónica
La media armónica es un promedio muy útil en conjuntos de números que se definen en relación con alguna unidad, por ejemplo la velocidad (distancia por unidad de tiempo).
Moda
En estadística, la moda es el valor con una mayor frecuencia en una distribución de datos. Se hablará de una distribución bimodal de los datos adquiridos en una columna cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es en la que encontramos tres modas. Si todas las variables tienen la misma frecuencia diremos que no hay moda.
Mediana
Existen dos métodos para el cálculo de la mediana: Considerando los datos en forma individual, sin agruparlos. Utilizando los datos agrupados en intervalos de clase.
Cantidad (N) impar de datos
Las calificaciones en la asignatura de Matemáticas de 39 alumnos de una clase viene dada por la siguiente tabla:
| Calificaciones | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Número de alumnos | 2 | 2 | 4 | 5 | 8 | 9 | 3 | 4 | 2 |
primero se hallan las frecuencias absolutas acumuladas 
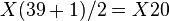. Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene 
.
. Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene .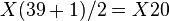
Rango
El Rango es el intervalo entre el valor máximo y el valor mínimo; por ello, comparte unidades con los datos. Permite obtener una idea de la dispersión de los datos, cuanto mayor es el rango, más dispersos están los datos de un conjunto.
No hay comentarios:
Publicar un comentario